Complex systems ranging from gene-regulatory networks to ecosystems and brain networks are evolving in time thanks to a combination of pairwise and higher-order interactions encoded in higher-order networks. However, in a large number of cases we have access only to pairwise interactions, while higher-order interactions are unknown. Thus developing new frameworks to mine higher-order interactions is one of the most significant challenges in the study of higher-order networks.  In [1] we propose for the first time an information theory framework to mine higher-order triadic interactions.

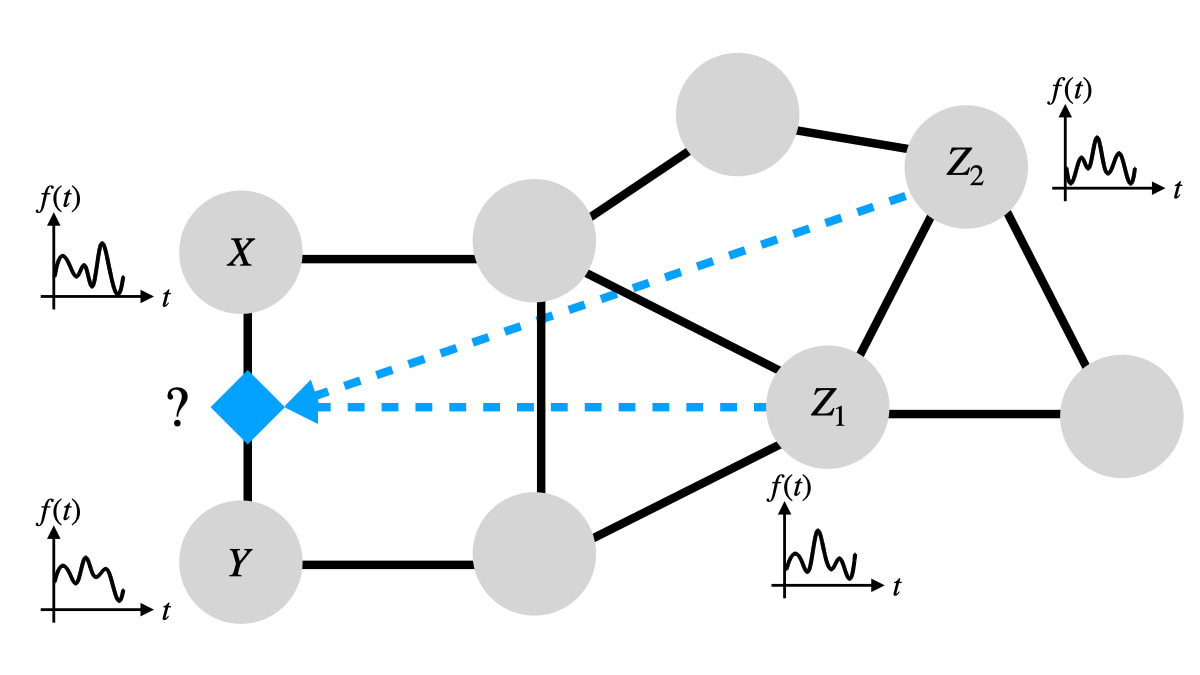
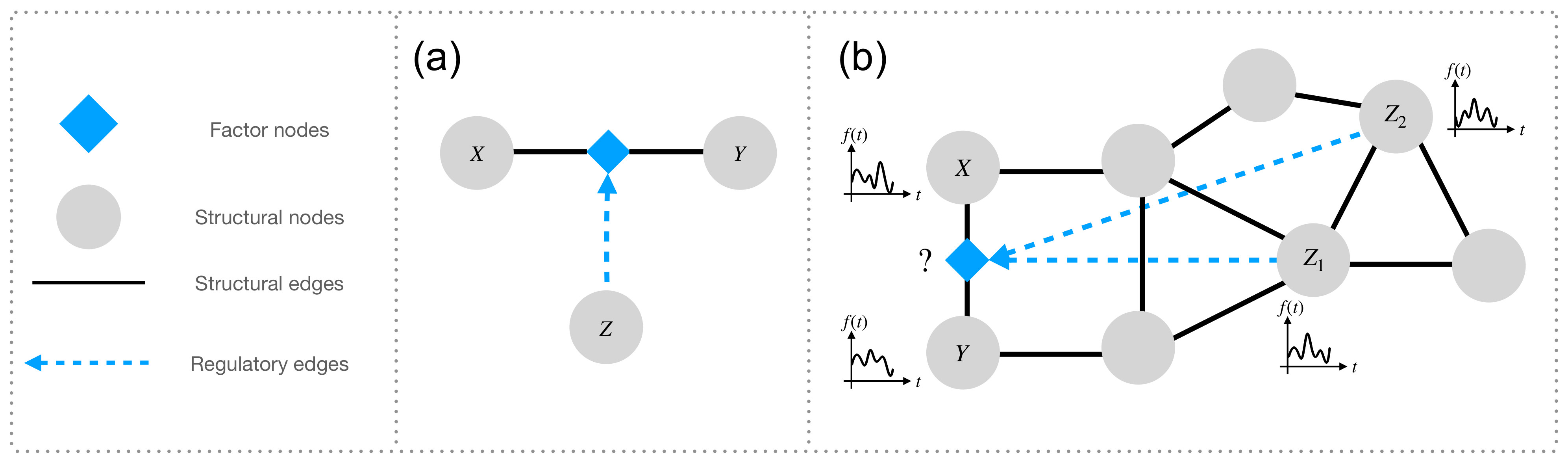
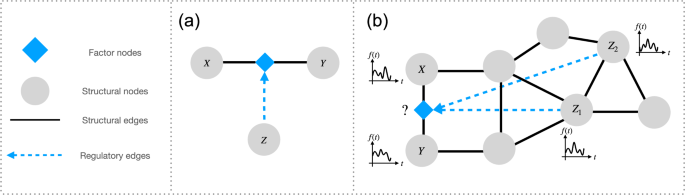
Higher-order triadic interactions [2-4] are a special type of higher-order interactions that occur when one or more nodes modulate the interaction between two connected nodes (see Figure 1).  Despite the increasing recognition of the importance of triadic interactions for many complex systems—from ecosystems to biological networks—methods for detecting such interactions directly from dynamical data have been lacking. 

In [1] we  propose the Triadic Perceptron Model (TPM) that captures the node dynamics in the presence of triadic interactions and reveals that triadic interactions modulate the mutual information between two linked  nodes.   Using this fundamental insight we demonstrate  that triadic interactions can be inferred by the Triadic Interaction Mining (TRIM) algorithm that  statistically  assesses the significance of the modulation of the mutual information between the two connected nodes.

The performance of TRIM is validated on the surrogate data generated with the TPM  and applied  to gene expression data, finding new candidates for triadic interactions relevant for Acute Myeloid Leukemia (AML).

This work opens new perspectives in inference of higher-order triadic interactions in complex systems across different domains including systems biology, neuroscience  and climate.

Results

The TPM model explicitly captures the regulation of the interaction between two nodes (X and Y) due to the regulatory interactions of the regulatory node  (Z) involved in the higher-order triadic interaction.

The model clearly reveals that the mutual information between the linked nodes X and Y  is modulated by the regulatory node Z when a triadic interaction is present, while this modulation is not observed if there is no triadic interaction (see Figure 2).

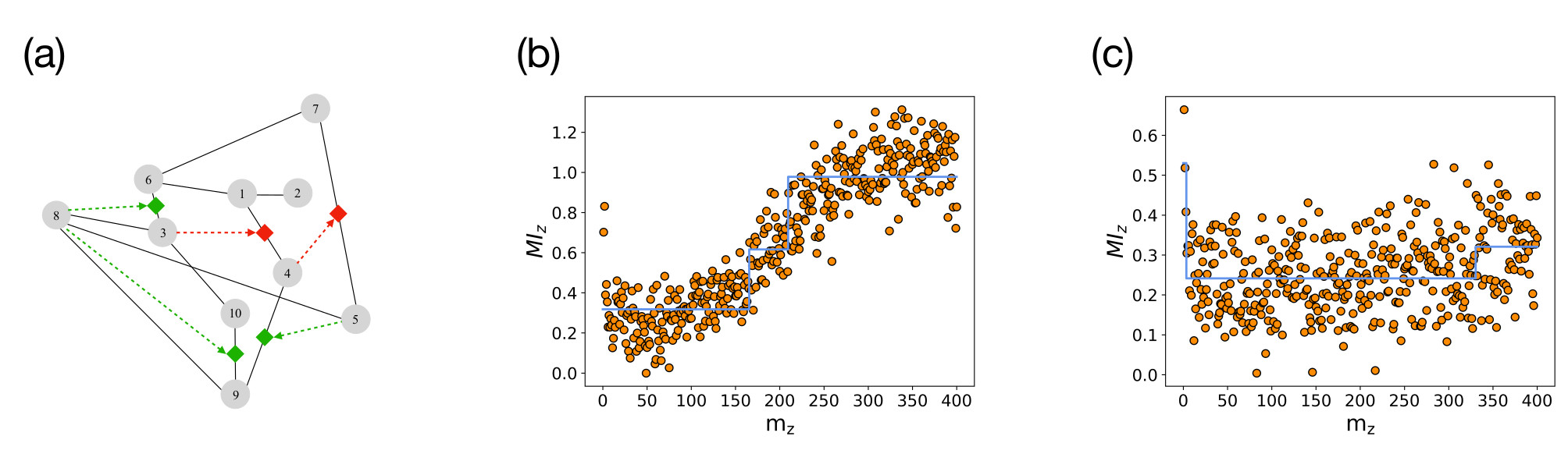
Building on this signature of triadic interactions we propose the  TRIM algorithm (see Figure 3). The TRIM algorithm starts from the knowledge of a pairwise network and the time series of the nodes and mines triadic interactions by assessing the significance of the modulation of the mutual information against two null models.

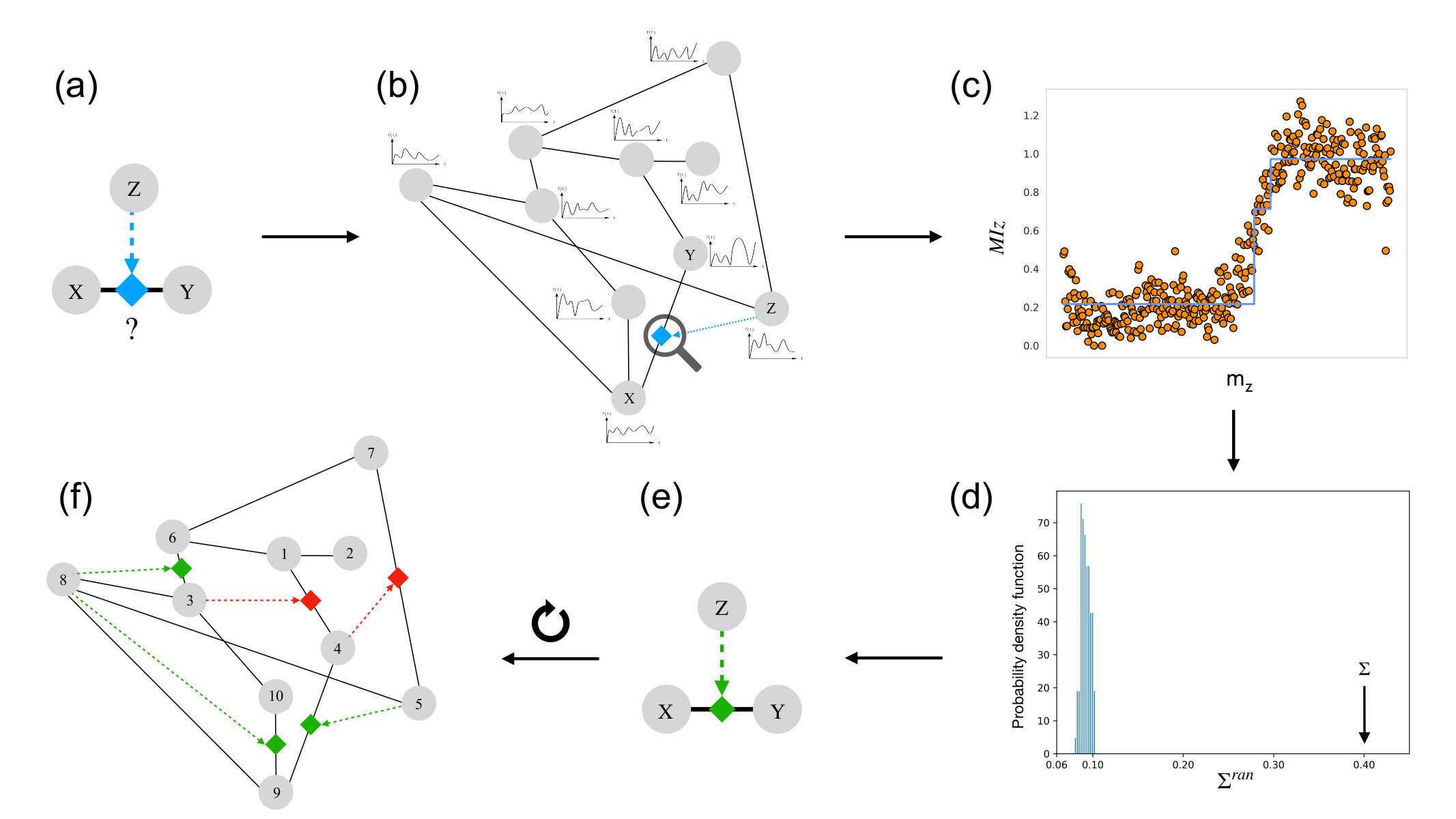
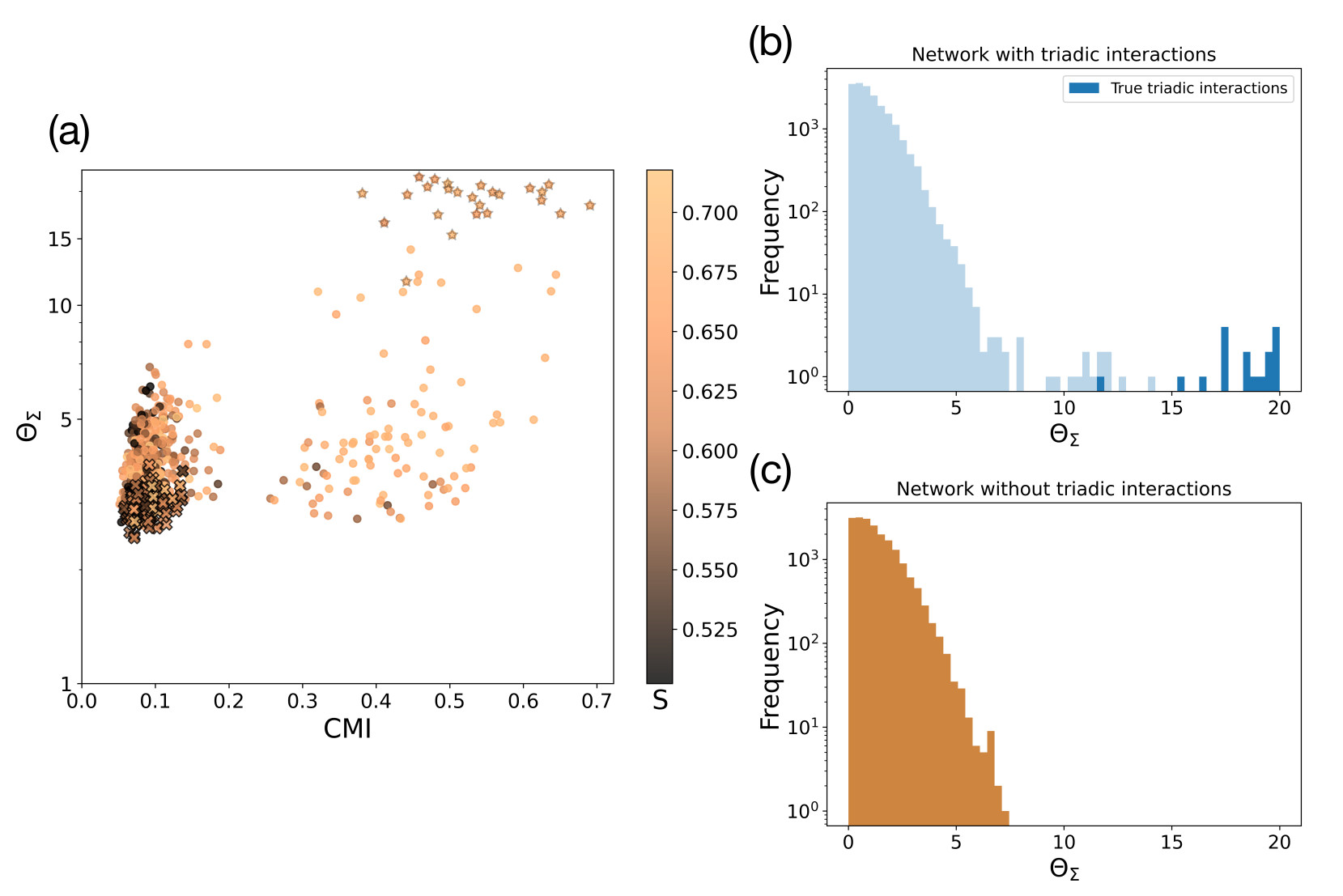
TRIM has an excellent performance on random graphs where the nodes' dynamics follows the TPM which allows us to validate the algorithm in a controlled setting. In particular the TRIM algorithm detects the true triadic interactions present in the data and clearly distinguish between a random network with and without triadic interactions (see Figure 4).

Finally, we apply the TRIM algorithm to the AML gene expression data proposing new candidates for triadic interactions that can be experimentally tested.

Overall, in [1] we provide a new dynamical model, the TPM, for treating node dynamics in the presence of triadic interactions, which demonstrates the role of the regulatory nodes in modulating the mutual information among linked nodes. The TRIM algorithm that we formulate in this work is based on this fundamental insight and is proven to efficiently mine triadic interactions in model generated data and in real-world datasets.

This work opens new perspectives in dynamical and information systems and in the study of complex networks and might find interesting applications across different scientific domains, including systems biology, climate, AI and neuroscience.

References

[1]  Niedostatek M, Baptista A, Yamamoto J, Kurths J, Garcia RS, MacArthur B, Bianconi G.,2025. Mining higher-order triadic interactions. Nature Communications, 16,11613 (2025)

[2] Sun, H., Radicchi, F., Kurths, J. and Bianconi, G. The dynamic nature of percolation on networks with triadic interactions. Nature Communications, 14, 1308 (2023).

[3] Grilli, J., Barabás, G., Michalska-Smith, M.J. and Allesina, S., Higher-order interactions stabilize dynamics in competitive network models. Nature, 54, 210-213 (2017).

[4]  Bairey, E., Kelsic, E.D. and Kishony, R.,  High-order species interactions shape ecosystem diversity. Nature Communications, 7, 12285 (2016).