In my view, birds of prey represent the pinnacle of evolution – combining power and grace with exceptional hunting abilities. I have really enjoyed studying the attack behaviours of hawks and falcons during my PhD and as a Post-doc in the Oxford Flight Group, not only in seeing these formidable predators in action, but being able to work in some great locations and experiencing new climates and wildlife. It has also been hugely rewarding - by revealing how birds of prey pilot their intercept trajectories my team and I have developed a new approach to studying natural behaviours and inspired a new generation of research into animal pursuit dynamics.

When intercepting a target, the relationship between visual stimuli (sensory input) and steering behaviour (motor output) can be explained by using repeatable, quantitative mappings – known as behavioural algorithms [1]. By modelling these algorithms on empirical trajectory data, I have been able to determine the manoeuvres used by birds of prey to pursue and intercept prey. During hunting exploits, hawks and falcons have been found to use simple proportional feedback controllers called guidance laws to adjust their course towards prey in closed-loop [2-6]. Proportional navigation (PN) guidance leads a predator to adjust its rate of turning in proportion to the change in the line-of-sight bearing that points from predator to prey [7]. Its simplicity may explain why PN, or similar feedback guidance laws, appear to have evolved across a diverse range of predators for intercepting prey – from birds [2, 8] and bats [9], to beetles [10], flies [3, 11] and fish [12] – however, these studies have only involved chases against single prey targets. The obvious next step was to ask how aerial predators, when faced with dense prey aggregations, overcome the sensory challenges posed by their collective motion to intercept a single individual?

Figure 1. Swainson’s hawk hunting Mexican Free-tailed bats. This photo was taken at the study site in New Mexico and provides a snap-shot of the sensory challenge faced by a predator attacking the swarm.

Although group formation is an extremely widespread phenomenon in nature, with more than 50% of fish and birds forming schools and flocks respectively, there are very few empirical studies relating the outcomes of attacks on three-dimensional prey aggregations to the individual behaviours of predators. This is presumably due to the challenges in quantifying the behaviours over appropriate temporal and spatial scales. Instead, the emphasis is usually placed on the predation risk experienced by the prey and the mechanisms for group formation [13-15]. Studies specifically focused on predatory behaviour have mainly looked at whether confusion effects explain their attack preferences [16]. The confusion theory states that having many similar prey-targets all visible simultaneously acts to divert the predator’s attention and affects their ability to aim at one individual [13]. Many laboratory experiments and field observations across different animal taxa support this theory, showing that predator attack efficiency decreases with increasing swarm size or density (e.g. [17-19]).

In a collaboration with Dr Laura Kloepper, from the Ecological Acoustics and Behavior Lab at the University of New Hampshire in the US, I had the opportunity to study the attack strategies of hawks hunting bats within massive aerial aggregations. Bats are not typical prey of hawks, but a small population of Swainson’s hawks (Buteo swainsoni) have specialized to prey upon a seasonal population of Mexican free-tailed bats (Tadarida brasiliensis) at a remote site in the Chihuahuan Desert in New Mexico (Fig.1) [20]. The study site is located on a vast volcanic plateau at approximately 1500 m altitude, where the remains of lava tubes form deep caves which the bats use as a day roost during their breeding season from May to September. The bat population consists of a maternal colony of approximately 700,000 to 900,000 individuals [21] which stream out at dusk en masse in a continuous ribbon to fly to their feeding grounds. The predictability and regularity of the behaviours make it an excellent study system (as long as you can successfully dodge the rattle snakes!).

I set out to investigate the targeting strategy used by the hawks when predating upon the bats as they departed from their roost. I used camera-pairs in stereo to reconstruct their 3D flight paths and analysed the trajectories mathematically by modelling candidate guidance algorithms on the observed attack behaviours. This is the same algorithmic approach as in previous pursuit studies, but applied to collective behaviour. However, the previous work assumed the predator responded to the instantaneous position of its prey, in what’s called a closed feedback-loop. Since a bat is a highly agile target that cannot be easily picked out from the swarm, we tested the assumption by modelling the guidance algorithms using the final position of the bat as a fixed virtual target point, as well as using the bat’s position history. After modelling all attacks, we found that PN simulations using the fixed point as the target fitted the data more closely overall than those targeting the bat’s instantaneous position (Fig.2). 

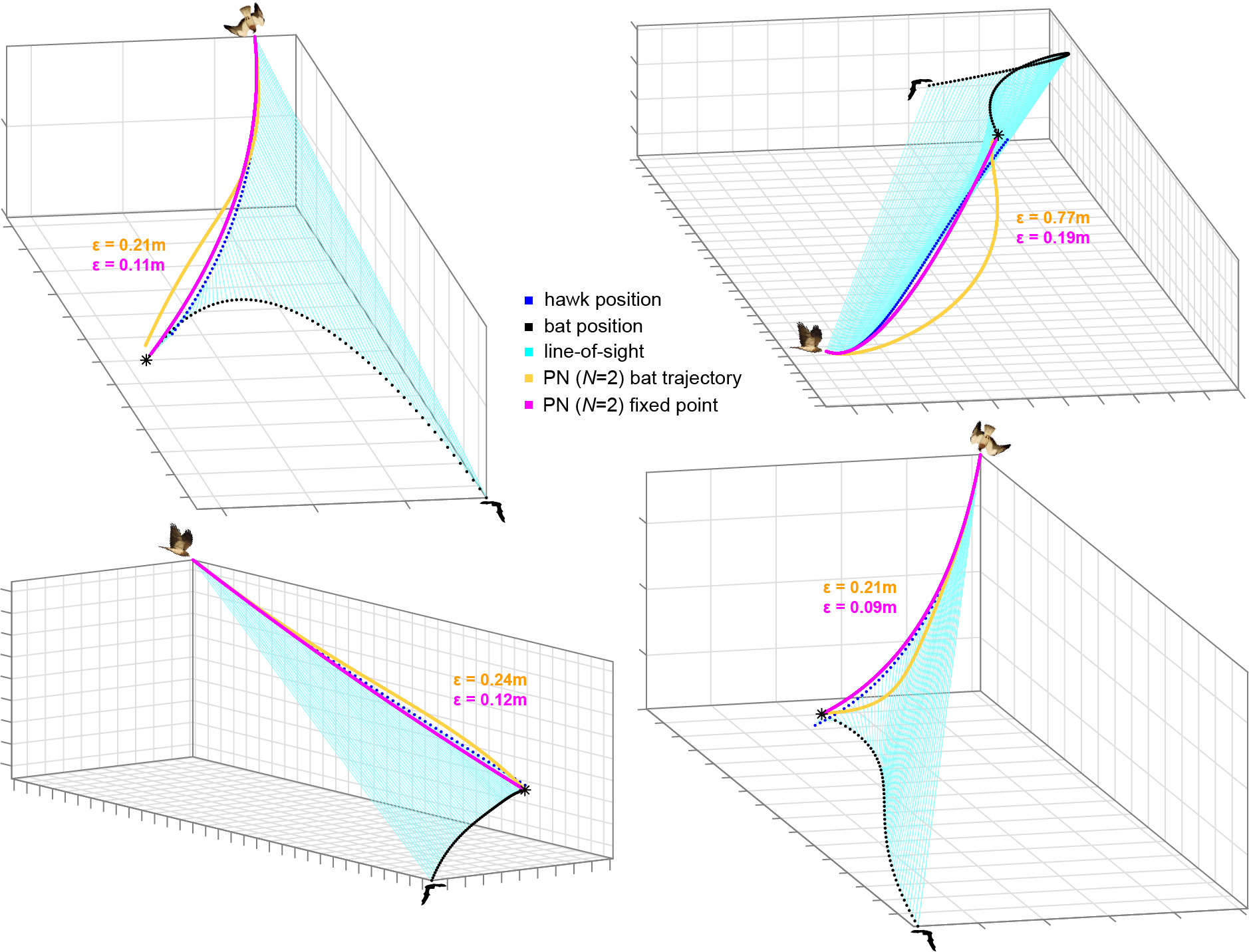
Figure 2. Reconstructed 3D attack trajectories of 4 successful Swainson’s hawks attacks on Mexican free-tailed bats, with guidance comparisons. The simulations of the hawk’s flight trajectory generated under PN guidance at a fixed navigation constant of N = 2, treating the final position of the bat as a fixed target (magenta) fitted the data more closely (lower error ε values) than those using the instantaneous position of the bat (orange). We used an N of 2 in order generate a constant radius turn that satisfies the kinematic constraint of passing through the hawk’s initial and final positions whilst also matching its initial flight velocity. The instantaneous line-of-sight (cyan) between the hawk and bat remains nearly parallel through time because they are on a collision course. Grid spacing: 1 m.

In contrast to raptors attacking single targets, the hawks do not engage in closed-loop pursuit of their prey, but instead target a spatially fixed point in the swarm. A remarkable feature of the hawks’ terminal attack trajectories is that the bearing of their line-of-sight to the bat remains nearly parallel throughout (Fig.3, 4A). This is because if two individuals are on a direct collision course, then the collision triangle remains geometrically similar through time. For our hawks, maintaining a constant bearing may substantially simplify the problem of identifying a single bat against the movement of the swarm. From the viewpoint of a stationary observer, all members of the swarm will appear to move erratically (Fig. 4B), whereas for a mobile observer, any member that it is on a collision course with will appear stationary against the residual movement of the swarm (Fig. 4C).

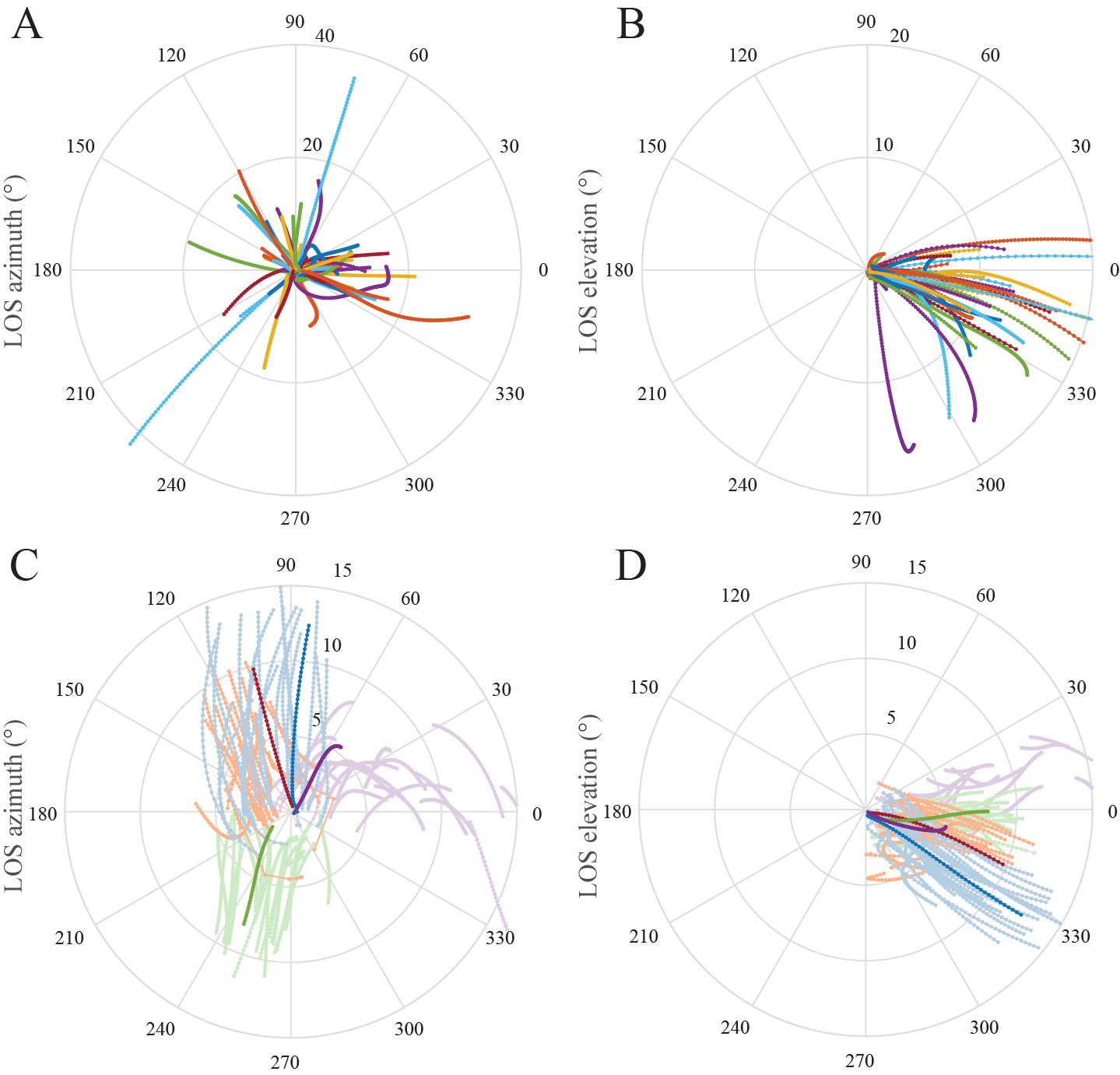
Figure 3. Constancy of line-of-sight angle during the final flight phase of Swainson’s hawks attacking Mexican free-tailed bats. (A,B) Polar plots displaying the azimuth and elevation of the line-of-sight (LOS) from the hawk to the bat it grabbed for all n=62 attacks; the radial coordinate represents the bat’s range. The plotted lines are nearly radial, indicating that the grabbed bat remains on a nearly constant bearing to the hawk. (C,D) Polar plots displaying LOS azimuth and elevation for 20 neighbouring bats tracked concurrently on each of four colour-coded attacks; darker lines display the LOS azimuth and elevation of the bat that was grabbed. These darker lines are more nearly radial than the lighter lines displaying the LOS azimuth and elevation of the neighbouring bats, confirming that the constant bearing geometry is specific to the grabbed bat.

In conclusion, I show how hawks avoid a confusion effect when attacking massive aggregations of swarming bats, as the constant bearing geometry of an incidental collision course simplifies the sensory challenge of identifying candidate targets (Fig. 4C). My results therefore suggest that the confusion effect may be less important to predators attacking dense swarms than has previously been assumed [22], and may also explain why some visually-guided predators, including raptors attacking bats [23], prefer to target larger or denser groups of prey. The findings also explain why neither the present study nor a previous study of the same model system [24] found any evidence that the bats’ swarming caused a reduction in the hawks’ hunting success when compared to attacks made at lone bats [24]. Therefore, this study system does not support the theory that predator hunting efficiency declines as group density increases due to the heightened sensory challenge [13]. Rather, my team and I propose that the very density of the swarm itself makes it possible that any swooping hawk will find itself on a collision course with a bat. This is, to my knowledge, the first time that three-dimensional trajectories have been reconstructed and analysed for wild predators and prey, and offers a first explanation of how dense prey aggregations that appear confusing to our own eyes do not necessarily result in a confusion effect in mobile predators. 

Figure 4. Mechanism by which the constant bearing geometry of an incidental collision course can avoid a confusion effect in a dense swarm. (A) Composite image showing the motion of a hawk (blue points) and the bat that it grabs from the swarm (black points), as seen from a fixed video camera. Note that the line-of-sight from the hawk to the bat (white lines) remains approximately parallel as the hawk plunges into the swarm, which is because the hawk is on a collision course with the bat that it grabs. (B) Example of the flight velocity (yellow arrows) of the bats (black points), as seen by a stationary observer. The projected flight velocity of the highlighted bat (red arrow) is used as a reference in the next panel. (C) Apparent velocity (cyan arrows) of the same bats, as seen by a moving observer whose translational motion makes the apparent velocity of the highlighted bat (red circle) zero, such that it appears stationary against the distant background. Whereas (B) represents the optic flow seen by a stationary observer, (C) represents the optic flow seen by a moving observer that happens to be on a collision course with the highlighted bat.

References

1. Hein, A.M., et al., An algorithmic approach to natural behavior. Current Biology, 2020. 30(11): p. R663-R675.
2. Brighton, C.H., A.L.R. Thomas, and G.K. Taylor, Terminal attack trajectories of peregrine falcons are described by the proportional navigation guidance law of missiles. Proceedings of the National Academy of Sciences of the United States of America, 2017. 114(51): p. 13495-13500.
3. Fabian, S.T., et al., Interception by two predatory fly species is explained by a proportional navigation feedback controller. Journal of the Royal Society Interface, 2018. 15(147).
4. Lohmann, A.C., A.J. Corcoran, and T.L. Hedrick, Dragonflies use underdamped pursuit to chase conspecifics. Journal of Experimental Biology, 2019. 222(11).
5. Olberg, R.M., et al., Eye movements and target fixation during dragonfly prey-interception flights. Journal of Comparative Physiology a-Neuroethology Sensory Neural and Behavioral Physiology, 2007. 193(7): p. 685-693.
6. Mills, R., et al., Physics-based simulations of aerial attacks by peregrine falcons reveal that stooping at high speed maximizes catch success against agile prey. Plos Computational Biology, 2018. 14(4): p. e1006044.
7. Shneydor, N.A., Missile guidance and pursuit: kinematics, dynamics and control. 1998: Woodhead Publishing Limited.
8. Brighton, C.H. and G.K. Taylor, Hawks steer attacks using a guidance system tuned for close pursuit of erratically manoeuvring targets. Nature Communications, 2019. 10.
9. Bar, N.S., et al., A sensory-motor control model of animal flight explains why bats fly differently in light versus dark. Plos Biology, 2015. 13(1).
10. Haselsteiner, A.F., C. Gilbert, and Z.J. Wang, Tiger beetles pursue prey using a proportional control law with a delay of one half-stride. Journal of the Royal Society Interface, 2014. 11(95).
11. Wardill, T.J., et al., A novel interception strategy in a miniature robber fly with extreme visual acuity. Current Biology, 2017. 27(6): p. 854-859.
12. McHenry, M.J., et al., The pursuit strategy of predatory bluefish (Pomatomus saltatrix). Proceedings of the Royal Society B-Biological Sciences, 2019. 286(1897).
13. Krause, J. and G.D. Ruxton, Living in groups. Oxford Series in Ecology and Evolution. 2002, Oxford: Oxford University Press.
14. Hamilton, W.D., Geometry for the selfish herd. Journal of Theoretical Biology, 1971. 31(2): p. 295-311.
15. Quinn, J.L. and W. Cresswell, Testing domains of danger in the selfish herd: sparrowhawks target widely spaced redshanks in flocks. Proceedings of the Royal Society B-Biological Sciences, 2006. 273(1600): p. 2521-2526.
16. Duffield, C. and C.C. Ioannou, Marginal predation: do encounter or confusion effects explain the targeting of prey group edges? Behavioral Ecology, 2017. 28(5): p. 1283-1292.
17. Kenward, R.E., Hawks and doves - factors affecting success and selection in goshawk attacks on woodpigeons. Journal of Animal Ecology, 1978. 47(2): p. 449-460.
18. Gillett, S.D., P.J. Hogarth, and F.E.J. Noble, Response of predators to varying densities of Gregaria locust nymphs. Animal Behaviour, 1979. 27(May): p. 592-596.
19. Milinski, M., Do all members of a swarm suffer same predation. Zeitschrift Fur Tierpsychologie-Journal of Comparative Ethology, 1977. 45(4): p. 373-388.
20. Baker, J.K., The manner and efficiency of raptor depredations on bats. American Ornithological Society, 1962. 64(6): p. 500-504.
21. Kloepper, L.N., et al., Estimating colony sizes of emerging bats using acoustic recordings. Royal Society Open Science, 2016. 3(3).
22. Jeschke, J.M. and R. Tollrian, Prey swarming: which predators become confused and why? Animal Behaviour, 2007. 74: p. 387-393.
23. Fenton, M.B., et al., Raptors and bats - threats and opportunities. Animal Behaviour, 1994. 48(1): p. 9-18.
24. Brighton, C.H., et al., Aerial attack strategies of hawks hunting bats, and the adaptive benefits of swarming. Behavioral Ecology, 2021. 32(3): p. 464-476.