Synchronization induced by directed higher-order interactions
Published in Physics
Network science is a powerful tool in the modeling of complex systems and its handy formalism has allowed scholars to dive into exciting topics such as pattern formation, data science and synchronization, just to name a few [1]. The latter in particular has triggered scholars before even network science was born, with the works of Pecora, Carroll and collaborators on chaotic circuits, leading to the Master Stability Function approach [2], which was later fully exploited thanks to the richness of possibilities given by network science.
In recent years, there has been a growing awareness that the network formalism, for how powerful, does not allow to fully capture the interactions within a system, as there may be many-body or higher-order interactions which are of a different nature and, consequently, need a different formalism. The community has hence converged towards the mathematical tools offered by hypergraphs and simplicial complexes, which saw an increasing interest and publications by scholars of the field [3]. Synchronization started to be studied on these higher-order structures and many interesting results have been obtained. In particular, a recent article on Nature Communications has proposed an elegant and powerful formalism to extend the Master Stability Function approach to simplicial complexes [4].
In our group at the Namur Institute for Complex Systems, we were already studying dynamics on networks, with particular focus on the effects of directed interactions on the dynamics. In fact, an important study, again from Nature Communications, showed the importance of such non-reciprocal interactions in systems coupled through networks [5]. We were indeed wondering if we could generalize higher-order interactions to account for asymmetry. Around the same time, we had the luck to start collaborating with some of the researchers who developed the Master Stability Function formalism on simplicial complexes from the University of Catania and after a while we realized that it could be extended to directed higher-order interactions as long as some symmetry properties were preserved. This lead to the idea of M-directed hypergraphs [6].
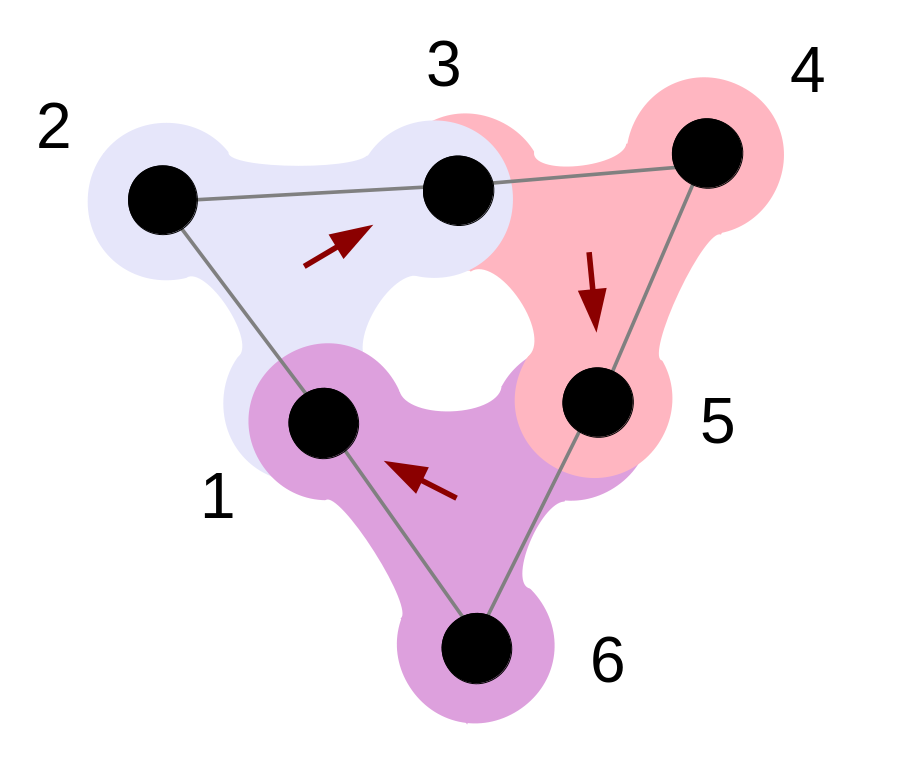
In a nutshell, let us consider an undirected hyperedge (of dimension 3 for simplicity). We can imagine the undirected interaction as the sum of three elementary directed ones, as shown in the Figure below, which illustrates an example of 1-directed hyperedges. If the interaction in the hyperedge would be directed towards m nodes, this would become an m-directed hyperedge. An M-directed hypergraphs is a hypergraphs whose hyperedges are m-directed with m at most M. Remarkably, such directed interactions preserved some symmetries in the formalism, which allow us to extend the Master Stability Function approach and to study the effects of directionality on synchronization. We observed that the directed higher-order interactions can destroy synchrony obtained when the interactions are symmetric, but sometimes directionality can help synchronize a system which would otherwise be desynchronized.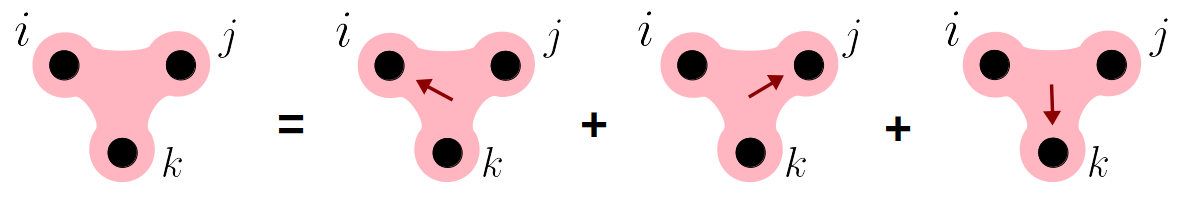
This formalism is just the beginning in the study of directed higher-order interactions and we believe it paves the way to new exciting discoveries.
I skipped all the mathematical nitty gritty, but you can find everything in the paper.
If you have any questions don't hesitate to reach out to us.
References
[1] Latora, V., Nicosia, V. & Russo, G. Complex networks: principles, methods and applications. (Cambridge University Press, Cambridge, 2017).
[2] Pecora, L. M. & Carroll, T. L. Master stability functions for synchronized coupled systems. Phys. Rev. Lett. 80, 2109 (1998).
[3] Battiston, F. et al. Networks beyond pairwise interactions: structure and dynamics. Phys. Rep., 874, 1–92, (2020).
[4] Gambuzza, L. V. et al. Stability of synchronization in simplicial complexes. Nat. Commun. 12, 1–13 (2021).
[5] Asllani, M. et al. The theory of pattern formation on directed networks. Nat. Commun. 5, 4517 (2014).
[6] Gallo, L. et al. Synchronization induced by directed higher-order interactions. Comm. Phys. 5, 263 (2022).
Follow the Topic
-
Communications Physics

An open access journal from Nature Portfolio publishing high-quality research, reviews and commentary in all areas of the physical sciences.
Related Collections
With Collections, you can get published faster and increase your visibility.
Higher-order interaction networks 2024
Publishing Model: Open Access
Deadline: Feb 28, 2026
Physics-Informed Machine Learning
Publishing Model: Hybrid
Deadline: May 31, 2026
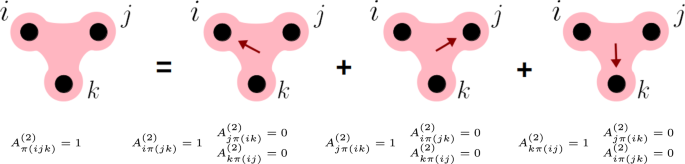

Please sign in or register for FREE
If you are a registered user on Research Communities by Springer Nature, please sign in