Unravelling Quantum Dynamics Using Flow Equations
Published in Physics

Accurately simulating the non-equilibrium dynamics of quantum matter on classical computers is a notoriously hard problem. Many powerful and innovative numerical methods have been developed to solve this problem in one dimension for reasonably large times, but few methods exist for the simulation of two-dimensional quantum systems. In a recent publication in Nature Physics, we have proposed a radical new method based on different principles to the existing state-of-the-art methods, and shown that it allows us to simulate the non-equilibrium dynamics of a certain class of large two-dimensional quantum systems to very long times.
The problem
Quantum systems are perhaps the most striking example of complex behavior arising from relatively simple ingredients. A single quantum bit – a qubit – can be in any linear combination of two possible states, typically labeled 0 and 1. Two qubits can be in any linear combination of four possible states (00,01,10, and 11), three qubits can be in superpositions of eight possible states, and so on. The number of orthogonal states rises exponentially with the number of particles, meaning that even powerful classical computers run out of memory when trying to simulate in full in their out-of-equilibrium properties more than a few tens of quantum particles. One possible way out of this quandary is the use of quantum computers, but current quantum computers are not yet powerful enough to outdo the very best classical simulations.
Scientists have known of this problem for decades, and several sophisticated techniques have been proposed to avoid this issue. There are also deep and fundamental obstructions that arise from theoretical computer science that indicate that there cannot be a universal classical algorithm that simulates the dynamics of local Hamiltonians for all times. This does not mean, however, that this problem is intractable for rich families of physically interesting problems. One of the most well-known is the use of tensor networks to represent certain quantum states in memory-efficient ways. These work extremely well for weakly entangled quantum systems in one dimension, but struggle to capture highly entangled quantum systems, which are arguably some of the most interesting and which generically appear for long times in simulations. This problem becomes much more challenging in two dimensions, where the even more rapid growth of entanglement threatens to quickly overwhelm even cutting-edge tensor network techniques.
Tensor networks are by no means the only game in town. Exciting progress is being made in the field of neural networks and machine learning, and new developments in this field are arriving quickly. Monte Carlo sampling techniques are employed, and so are dynamical mean field ansatzes. The vast majority of conventional approaches all share the same underlying philosophy. They typically work by manipulating a single quantum state, often evolving it in time to compute non-equilibrium dynamics, or trying to minimize its energy and find what is known as the ‘ground state’ (the lowest energy configuration of the quantum system). Even algorithms designed to run on cutting-edge quantum computers usually work in this way, varying a single state at a time.
Instead of taking this route, we instead ask a different question – what if we could solve the quantum problem for all possible states at once?
Our approach
In our recent work, we demonstrate a novel way to solve this problem. Rather than evolving a single state in time, as in most numerical methods, we instead try to transform the problem into the simplest possible form (known as ‘diagonalisation’), at which point it becomes possible (if not always easy!) to compute anything we want.
We start by encoding the quantum system of interest as a series of tensors, which can be thought of as high-dimensional arrays of numbers. The dimension of each tensor is given by the number of (in our case, fermionic) operators in the corresponding term in the Hamiltonian. We then ‘simplify’ the problem using a series of unitary operations, which are equivalent to rotations in a high dimensional space.

A helpful analogy is to imagine starting from a Rubik’s cube with the faces arranged in a highly structured way (where the structure encodes the initial physical problem), and trying to find the sequence of rotations that solve it. In mathematical terms, this sequence of rotations we make is called a continuous unitary transform. It turns out that the computations required to work out the sequence of rotations can be performed very efficiently on graphics processing units (GPUs), which enable us to perform the large number of calculations extremely quickly.
These have been used to study many-body quantum systems before, but until now, they have always had one major limitation. If you have ever tried solving large Rubik’s cubes (e.g. the 4x4x4 cube), you might be familiar with what’s known as the ‘parity problem’. This occurs when a sequence of seemingly-correct rotations takes you into a dead-end, and sometimes the easiest way out is to scramble the cube and start again. A similar thing happens with continuous unitary transforms; in certain scenarios, they can completely fail.
The solution is almost exactly the same as in the case of the humble Rubik’s cube: we scramble the problem up and start again in a new configuration that’s easier to solve. Initially, we started by making a sequence of completely random rotations, which we called scrambling transforms, however we soon realized that this was overkill for most approaches. In the end, we discovered that we could often use more carefully tailored rotations to remove only the problematic parts without having to completely start again. We were able to combine this with a rigorous mathematical guarantee as to the accuracy of the technique, verifying that it is accurate as well as performant.
Our results
The combination of powerful GPUs to do the computational heavy-lifting and the development of scrambling transforms to widen the validity of the method has been transformative. In order to illustrate this, we chose to demonstrate the method on a challenging modern problem known as many-body localization (MBL).
We simulated large systems of interacting fermions moving in randomly disordered environments, as well as quasi-disordered environments. It is believed that sufficiently strong disorder will prevent the quantum particles from being able to move, making MBL a promising candidate for the development of future quantum memories. Recently, however, doubts have been cast on whether this is true or just an artefact of early numerical simulations on small systems.
We have performed some of the largest simulations to date. Our results show that in one dimension, localization remains stable for exceedingly long times, while in two dimensions localization is far more stable in quasi-disordered systems than in truly random ones. While we cannot definitively say whether MBL is stable for infinitely long times, we are able to show that it is stable for a long enough time to be of practical use.
Outlook
Our work opens a door for the further development of computational methods involving continuous unitary transforms, and as with any new method there remains enormous scope for further development, improvement and extension. Although the method works on principles different to existing techniques, we believe that the best way forward will be to combine aspects of our work with other methods, for example incorporating the powerful representation of tensor networks to more efficiently compute the sequence of rotations we need, or making use of data-driven machine learning approaches to efficiently discover the optimum sequence of rotations. It is our hope that our work stimulates such further endeavours.
Follow the Topic
-
Nature Physics

This journal publishes papers of the highest quality and significance in all areas of physics, pure and applied.
Ask the Editor – Space Physics, Quantum Physics, Atomic, Molecular and Chemical Physics
Got a question for the editor about Space Physics, Quantum Physics, Atomic, Molecular and Chemical Physics? Ask it here!
Continue reading announcement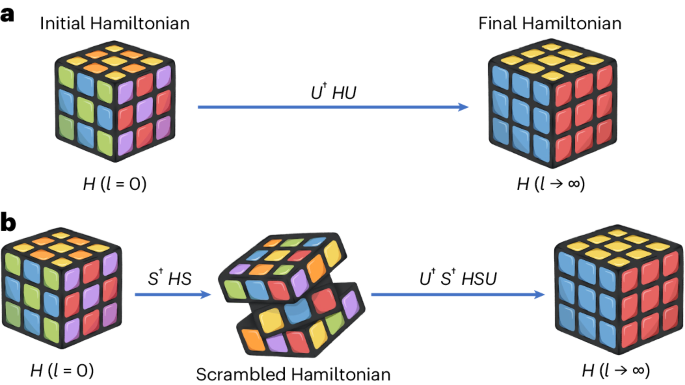
Please sign in or register for FREE
If you are a registered user on Research Communities by Springer Nature, please sign in