The evolutionary games played by cancer
Published in Ecology & Evolution
Of the maladies that plague us, cancer is one of the most devastating. The uncontrolled growth of cancerous cells and their metastases across the body can feel like an invasion from within. As the cells proliferate, they pass on the mutations and other aberrations that they’ve accumulated. Cancer evolves inside us. And it is this evolution that makes cancer such a formidable adversary for oncologists.
As a tumour grows, its various subclones interact with each other, and co-opt and compete against our healthy tissue. This makes cancer an ecological process. And it is this ecology that makes cancer so hard to predict.
Evolutionary game theory (EGT) lets us reason about ecological and evolutionary processes. This has allowed a branch of mathematical oncology to develop focused on the EGT of cancer. It is this connection to EGT that first brought me to the Moffitt Cancer Center. Before Moffitt, I felt that my work was too theoretical, and I wanted my research to have a more direct impact on people’s lives. So what better place could I pick to work than a cancer hospital?
During my time at Moffitt, I was given the opportunity to learn about the complexity of cancer and the counter-intuitive ideas that EGT could contribute to cancer treatment. Working with David Basanta and Jacob Scott, I was able to show that the spatial heterogeneity between the tumour boundary and bulk affected dynamics in a way that could hide invasive cells from detection by biopsies. Adding Robert Vander Velde to the team, we showed that certain systems of three cancer cell types could achieve a dynamic heterogeneity than one would not expect from any pair of interactions. This cycling heterogeneity was especially important for using evolution against cancer. Instead of treating the player, we could target the game (i.e. interaction between cells) and let evolution drive down undesirable rare cancer subtypes before targeting the most common subtype. Finally, in work led by Pranav Warman – now at Duke University – we could optimize adaptive therapies that use the evolution that happens naturally during treatment holidays to resensitize the tumour to our primary therapy.
This work was very exciting and relatively representative of the theoretical work being done for EGT in mathematical oncology. But one thing really bothered me: how were we figuring out the evolutionary games that defined these models?
As with most of the work in mathematical oncology, the games were based on physical and biological intuitions about what is happening between individual cells within the tumour. For example, when David, Jake and I looked at the Go vs Grow game in the context of edge effects, we assumed that invasiveness (Go) came at a fitness cost when up against autonomous growth cells (Grow). Or in the context of Pranav’s work on prostate cancer, we supposed – as many do – that drug resistance carries a cost. These were reasonable assumptions. But they were assumptions. Nobody had directly measured the payoff matrices that define the games of actual cancer systems. Given how misleading our intuitions about microscopic systems can be, this seemed like a big oversight for our community to not know the actual games that cancers play.
As I prepared to leave Moffitt and move to the University of Oxford, my job felt half-done. Jake was also preparing for his move to the Cleveland Clinic and shared my feeling. So as a last going-away push, we teamed up with two experimentalists – Jeffrey Peacock and Andriy Marusyk to get some closure. We set out to directly measure an evolutionary game in cancer.
The first step was to get all our concepts sorted out. To figure out precisely: what are we going to measure? When we are building mathematical or computer models, it is easy to imagine ourselves at the level of individual cells and to specify important parameters – such as the game payoffs – at this reductive level. When we are coding simulations, for example, we specify the fitness effect of interaction on individual cells and imagine that ‘payoff’ as coming from the interaction of a pair of cells (two ‘tokens’). But this isn’t a level that experimentalists usually measure at. Instead, we knew that our measurements would be at the level of populations of cells. Thus, we would be measuring not the interaction of two specific tokens (the reductive game), but rather an abstract interaction between two types of cells. We would be measuring an effective game.
With this cleared up, developing an actual game assay to measure the evolutionary game was relatively straightforward. Co-culture experiments were already the gold standard in microbiology, although less often used cancer biology – so we just needed to find two different cancer strategies and measure their fitness in co-culture with various initial proportions of the two types. From how the fitness changed with initial proportion we could then infer a fitness function and that fitness function would specify the game. And with the addition of just a pinch of math, we could propagate our measurement errors across all these levels of analysis to get a final point in game-space along with error bars. This was our game assay.
With the conceptual analysis sorted out and measurement methodology developed, we need to actually pick which cancer to focus on. Here, it was largely happenstance: Jake happened to be already working on non-small cell-lung cancer as part of a study of collateral sensitivity to various drugs. As such, he had handy some cell lines with evolved resistance to Alectinib. Based on the existing experimental literature, Jeff and Andriy suspected that it might have at least some interesting interactions with fibroblasts – a non-cancerous cell that is often co-opted by tumours. So, we had our system: two cancer strategies (drug-sensitive and drug-resistant) and two environmental variables: (absence/presence of drug; and absence/presence of cancer-associated fibroblasts).
The last experimental ingredient was the measure of fitness. Thankfully at Moffitt, we had a well-appointed imaging core that could provide time-lapsed fluorescent microscopy of our in vitro system. We tagged the two cancer strategies with different fluorescent proteins and ran the co-culture competition experiments. I could then write the computer vision code to quantify the two types’ population sizes and turn the resulting population size vs. time data into an estimate of growth rate. This growth rate was our measure of fitness.
By the time that Jake and I left Moffitt in 2016, we had run the experiments. Only the analysis and writing was left. By August, 2017 we had our first public draft out on BioRxiv. Finally, early in 2019, we shared our results in the pages of Nature Ecology and Evolution.
So, what did we learn?
Frequency dependence and evolutionary games matter to our study of cancer. But most of the intuitions we have about these games are wrong. Or, at least, our intuitions need some refinement.
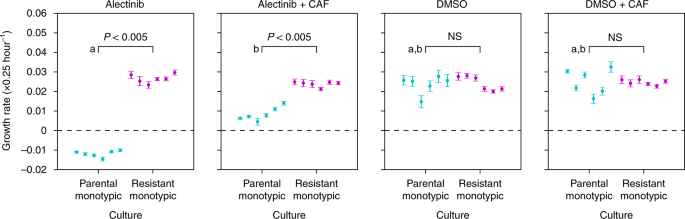
We observed two different types of games in our non-small cell lung cancer system. In three of the conditions (drug with or without fibroblasts, and no drug with no fibroblasts) we measured the Deadlock game. In the remaining condition of no drug but with fibroblasts, we saw the Leader game. And as far as I know, neither of these games has ever been studied in the context of mathematical oncology. They are simply not ‘exciting enough’ from a theory perspective – this is because they don’t make interesting reductive games for simulations.
But the games we measured are effective games. This means that population structures like space could transform theoretically exciting reductive games into these measured effective games. For example, under the model of space we used in our theoretical study of edge effects in the Go vs Grow game, the theoretically exciting Hawk-Dove game is transformed into the Leader game that we measured in non-small-cell lung cancer. Inverting the typical pipeline of reductive to effective games and thinking from effective games to reductive games is new ground for mathematical oncologists. I expect that it will yield new and exciting game theory to accompany our empirical measurements.
More importantly for the non-game-theorist, the games we measured challenge our standard intuitions about costly resistance. For example, when Pranav Warman and I had studied adaptive therapy, we assumed – as most people tend to do – that resistance was costly. But now we had a measurement. In our non-small cell lung cancer, resistance was not costly.
If we had studied only monocultures, then we would have concluded – as a few experimentalists before us – that resistance had no cost: parental cell and resistant cells in monoculture grew at about the same rate. But this wasn’t the case when they were mixed together in co-culture. In co-culture, the resistant cells consistently outperformed their parental co-habitants. And – in most conditions – as the proportion of parental decreased, so did the fitness of both the parental and resistant cells, at about the same rate. This happened in both the presence and absence of drug. In other words, even in the control condition (DMSO), resistant cells could outperform parental cells in co-culture.
This has important consequences for how we think about treatment and the debate between maximum tolerable dose and adaptive therapy. How would we do adaptive therapy when there is a ‘negative’ cost to resistance? And if we cannot then how do we identify which cancers have classic costs of resistance versus these new ‘negative’ costs that we observed? These questions will need to be resolved in order to understand when adaptive therapy will and won't be useful. And it is this development that recently caused Eric Topol to deem our paper as one of the 15 evidentiary shakeups that challenged biomedical dogma in 2019. I was very happy about this recognition.
But the most exciting result from our experiments – at least for me – was in the case of DMSO + fibroblasts. Apart from verifying that fibroblasts help protect the cancer from drug, we also showed that the game in that condition is qualitatively different from the other three cases. It was the Leader game instead of Deadlock. This meant that adding drug or eliminating fibroblasts not only quantitatively changed the ecological dynamics but qualitatively changed the kind of ecological dynamics. In other words, we were able to experimentally demonstrate a central concept of EGT in oncology: don’t treat the player, treat the game. Before, it was taken as a theoretical postulate that certain drugs or other interventions could transform an evolutionary game into a qualitatively different kind. For example, we made this assumption with vascular renormalization therapy and buffer therapy in our work with Robert Vander Velde. But now, we had an empirical demonstration that these sorts of qualitative shifts in ecology are possible.
Unfortunately, in our system both kinds of dynamics would be bad for a patient. So lots of work remains to be done. Thankfully, Jake has recently secured an R01 grant to push this work forward and I have received a fellowship from the James S. McDonnell Foundation to combine this work with my other work on algorithmic biology. Now, we can start building a catalog of evolutionary games in cancer and learn the consequences of these games for cancer’s evolution. My hope is that eventually these clearer measurements of the games played by cancer will lead us to new understanding and – more importantly – new treatments for this malady.
Follow the Topic
-
Nature Ecology & Evolution

This journal is interested in the full spectrum of ecological and evolutionary biology, encompassing approaches at the molecular, organismal, population, community and ecosystem levels, as well as relevant parts of the social sciences.
Related Collections
With Collections, you can get published faster and increase your visibility.
Biodiversity and ecosystem functioning of global peatlands
Publishing Model: Hybrid
Deadline: Jul 27, 2026
Understanding species redistributions under global climate change
Publishing Model: Hybrid
Deadline: Jun 30, 2026

Please sign in or register for FREE
If you are a registered user on Research Communities by Springer Nature, please sign in